Lãi đơn và lãi kép: Định nghĩa và công thức

Lãi đơn so với lãi kép: Tổng quan

Lãi suất được định nghĩa là chi phí vay tiền. Nó cũng có thể là lãi suất phải trả cho khoản tiền gửi, như trong trường hợp chứng chỉ tiền gửi. Lãi suất có thể được tính theo hai cách: lãi đơn hoặc lãi kép

Lãi đơn được tính trên số tiền gốc hoặc số tiền ban đầu của khoản vay.

Lãi kép được tính dựa trên số tiền gốc và lãi tích lũy từ các kỳ trước và do đó có thể được gọi là “lãi trên lãi”.

Có thể có sự chênh lệch lớn về số tiền lãi phải trả cho một khoản vay nếu lãi suất được tính theo phương pháp lãi kép thay vì phương pháp lãi đơn. Nhưng phép màu của lãi kép có thể mang lại lợi thế cho bạn khi đầu tư. Nó có thể là một yếu tố mạnh mẽ trong việc tạo ra của cải.

Lãi đơn và lãi kép là những khái niệm tài chính cơ bản, nhưng việc hiểu rõ chúng có thể giúp bạn đưa ra quyết định sáng suốt hơn khi vay vốn hoặc đầu tư. Lãi tích lũy cũng có thể giúp bạn lựa chọn đầu tư trái phiếu.

Công thức lãi đơn

Công thức tính lãi đơn là:

Lãi suất đơn giản = P × i × N

trong đó:

P = Vốn gốc

i = Lãi suất

N = Thời hạn vay

Tổng số tiền lãi mà người vay phải trả được tính là 10.000 đô la x 0,05 x 3 = 1.500 đô la nếu lãi suất đơn được tính là 5% cho khoản vay 10.000 đô la trong ba năm. Lãi suất của khoản vay này là 500 đô la mỗi năm hoặc 1.500 đô la trong suốt thời hạn vay ba năm.

Công thức lãi kép

Công thức tính tổng số tiền phải trả cho một khoản vay có lãi kép là:

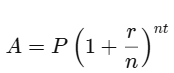
A = Tổng số tiền cuối cùng sau khi tất toán lợi nhuận

P = Số dư gốc ban đầu

r = Lãi suất

N = Số lần áp dụng lãi suất theo từng khoảng thời gian

t = Khoảng thời gian đã trôi qua

Lãi kép bằng tổng số tiền gốc và lãi trong tương lai, hay giá trị tương lai , trừ đi số tiền gốc hiện tại, được gọi là giá trị hiện tại (PV). PV là giá trị hiện tại của một khoản tiền hoặc dòng tiền trong tương lai với một tỷ lệ hoàn vốn cụ thể.

Số tiền lãi trong ví dụ về lãi đơn sẽ là bao nhiêu nếu được tính theo lãi kép?

Tổng số tiền lãi phải trả trong ba năm của khoản vay này là 1.576,25 đô la, không giống như lãi suất đơn, nhưng số tiền lãi không giống nhau trong cả ba năm vì lãi suất kép còn tính đến lãi suất tích lũy của các kỳ trước. Lãi suất phải trả vào cuối mỗi năm được hiển thị như sau:

Kỳ tính lãi kép

Số kỳ tính lãi kép tạo ra sự khác biệt đáng kể khi tính lãi kép. Số kỳ tính lãi kép càng cao thì số tiền lãi kép thường càng lớn.

Số tiền lãi tích lũy ở mức 10% hàng năm sẽ thấp hơn lãi suất tích lũy ở mức 5% hai lần một năm cho mỗi 100 đô la vay trong một khoảng thời gian nhất định. Điều này cũng sẽ thấp hơn lãi suất tích lũy ở mức 2,5% hàng quý.

Các biến “i” và “n” trong ngoặc đơn phải được điều chỉnh trong công thức tính lãi kép nếu số kỳ tính lãi kép nhiều hơn một lần trong năm.

“I” hay lãi suất phải được chia cho “n”, số kỳ tính lãi kép mỗi năm. “N” phải được nhân với “t”, tổng thời hạn đầu tư, ngoài dấu ngoặc đơn. Vậy i = 5% (tức là 10% ÷ 2) và n = 20 (tức là 10 x 2) đối với khoản vay 10 năm với lãi suất 10%, trong đó lãi được tính lãi kép nửa năm một lần: số kỳ tính lãi kép = 2.

Bạn sẽ sử dụng phương trình này để tính tổng giá trị với lãi kép:

trong đó:

P = Vốn gốc

i = Lãi suất tính theo phần trăm

N = Số kỳ tính lãi kép mỗi năm

t = Tổng số năm đầu tư hoặc vay

Bảng này minh họa sự khác biệt về số kỳ tính lãi kép theo thời gian đối với khoản vay 10.000 đô la trong thời hạn 10 năm.

Các khái niệm lãi kép khác

Lãi kép không chỉ liên quan đến các khoản vay.

Giá trị thời gian của tiền

Tiền không “miễn phí” mà có chi phí về lãi suất phải trả, do đó, một đô la hôm nay có giá trị hơn một đô la trong tương lai. Khái niệm này được gọi là giá trị thời gian của tiền tệ , và nó tạo thành cơ sở cho các kỹ thuật tương đối tiên tiến như phân tích dòng tiền chiết khấu (DFC).

Ngược lại với lãi kép được gọi là chiết khấu . Hệ số chiết khấu có thể được coi là nghịch đảo của lãi suất. Đó là hệ số mà giá trị tương lai phải được nhân với nó để có được giá trị hiện tại. Các công thức để tính giá trị tương lai (FV) và giá trị hiện tại (PV) là:

Trong đó:

i = Lãi suất tính theo phần trăm

N = Số kỳ tính lãi kép mỗi năm

t = Tổng số năm đầu tư hoặc vay

Quy tắc 72

Quy tắc 72 tính toán thời gian gần đúng mà một khoản đầu tư sẽ tăng gấp đôi với một tỷ lệ lợi nhuận hoặc lãi suất nhất định “i”. Quy tắc này được biểu thị bằng (72 ÷ i). Quy tắc này chỉ có thể được sử dụng để tính lãi kép hàng năm, nhưng có thể rất hữu ích trong việc lập kế hoạch số tiền bạn có thể có khi nghỉ hưu.

Một khoản đầu tư có tỷ lệ hoàn vốn hàng năm là 6% sẽ tăng gấp đôi sau 12 năm (72 ÷ 6%). Một khoản đầu tư có tỷ lệ hoàn vốn hàng năm là 8% sẽ tăng gấp đôi sau 9 năm (72 ÷ 8%).

Tỷ lệ tăng trưởng kép hàng năm (CAGR)

Tỷ lệ tăng trưởng kép hàng năm (CAGR) được sử dụng cho hầu hết các ứng dụng tài chính yêu cầu tính toán một tỷ lệ tăng trưởng duy nhất trong một khoảng thời gian.

Tỷ lệ tăng trưởng kép hàng năm (CAGR) là bao nhiêu nếu danh mục đầu tư của bạn tăng từ 10.000 đô la lên 16.000 đô la trong năm năm? PV = 10.000 đô la, FV = 16.000 đô la và nt = 5, vậy biến "i" cần được tính toán. Có thể chứng minh i = 9,86% bằng máy tính tài chính hoặc bảng tính Excel .

Khoản đầu tư ban đầu (PV) của bạn là 10.000 đô la được biểu thị bằng dấu âm, theo quy ước dòng tiền, vì nó thể hiện dòng tiền chảy ra. PV và FV nhất thiết phải có dấu ngược nhau để giải quyết vấn đề "i" trong phương trình trên.

Ứng dụng trong đầu tư

CAGR được sử dụng rộng rãi để tính toán lợi nhuận theo thời gian cho cổ phiếu, quỹ tương hỗ và danh mục đầu tư. Nó cũng được sử dụng để xác định liệu một nhà quản lý quỹ tương hỗ hoặc nhà quản lý danh mục đầu tư có vượt quá tỷ suất lợi nhuận của thị trường trong một khoảng thời gian hay không.

Một nhà quản lý quỹ được coi là hoạt động kém hiệu quả hơn thị trường nếu chỉ số thị trường mang lại tổng lợi nhuận là 10% trong năm năm, nhưng nhà quản lý đó chỉ tạo ra lợi nhuận hàng năm là 9% trong cùng kỳ.

CAGR cũng có thể được sử dụng để tính toán tốc độ tăng trưởng dự kiến của danh mục đầu tư trong dài hạn. Điều này hữu ích cho các mục đích như tiết kiệm hưu trí. Hãy xem xét các ví dụ sau:

Một nhà đầu tư ngại rủi ro hài lòng với mức lợi nhuận hàng năm khiêm tốn 3% cho danh mục đầu tư của mình. Do đó, danh mục đầu tư 100.000 đô la hiện tại của họ sẽ tăng lên 180.611 đô la sau 20 năm. Nhưng một nhà đầu tư chấp nhận rủi ro kỳ vọng mức lợi nhuận hàng năm 6% cho danh mục đầu tư của mình sẽ thấy 100.000 đô la tăng lên 320.714 đô la sau 20 năm.

CAGR có thể được sử dụng để ước tính số tiền cần phải tích lũy để tiết kiệm cho một mục tiêu cụ thể. Một cặp vợ chồng muốn tiết kiệm 50.000 đô la để trả trước cho một căn hộ trong 10 năm sẽ phải tiết kiệm 4.165 đô la mỗi năm nếu họ giả định lợi nhuận hàng năm (CAGR) là 4% từ khoản tiết kiệm của mình. Họ sẽ phải tiết kiệm 3.975 đô la mỗi năm nếu họ sẵn sàng chấp nhận rủi ro bổ sung và kỳ vọng CAGR là 5%.

CAGR cũng có thể được sử dụng để chứng minh lợi ích của việc đầu tư sớm hơn là muộn. Một người 25 tuổi sẽ phải tiết kiệm 6.462 đô la mỗi năm để đạt được mục tiêu nếu mục tiêu là tiết kiệm 1 triệu đô la khi nghỉ hưu ở tuổi 65, dựa trên CAGR là 6%. Một người 40 tuổi sẽ phải tiết kiệm 18.227 đô la, tức gần gấp ba lần số tiền đó, để đạt được mục tiêu tương tự.

Các ngân hàng và tổ chức tài chính có phương pháp chuẩn hóa để tính lãi suất phải trả cho các khoản thế chấp và các khoản vay khác, nhưng cách tính có thể hơi khác nhau ở mỗi quốc gia.

Những cân nhắc bổ sung

Hãy đảm bảo bạn biết chính xác tỷ lệ phần trăm hàng năm (APR) cho khoản vay của mình vì phương pháp tính toán và số kỳ tính lãi kép có thể ảnh hưởng đến khoản thanh toán hàng tháng của bạn.

Lãi kép có thể có lợi cho bạn khi đầu tư, nhưng cũng có thể có lợi khi bạn trả nợ vay. Trả một nửa số tiền thế chấp hai lần một tháng thay vì trả toàn bộ một lần một tháng sẽ giúp rút ngắn thời gian khấu hao và tiết kiệm cho bạn một khoản lãi đáng kể.

Tuy nhiên, lãi kép có thể gây bất lợi cho bạn nếu bạn đang vay những khoản lãi suất rất cao như nợ thẻ tín dụng hoặc nợ cửa hàng bách hóa. Số dư thẻ tín dụng 25.000 đô la với lãi suất 20% tính lãi kép hàng tháng sẽ dẫn đến tổng phí lãi là 5.485 đô la trong một năm, tương đương 457 đô la mỗi tháng.

Tôi sẽ sử dụng điều này như thế nào trong cuộc sống thực?

Hiểu rõ những tác động của việc sử dụng lãi suất đơn hay lãi suất kép sẽ giúp bạn đưa ra quyết định tài chính tốt hơn. Nếu bạn vay tiền, việc biết cách tính lãi suất sẽ cho phép bạn lựa chọn các điều khoản vay tốt nhất và tránh phải trả quá nhiều lãi suất.

Ví dụ, nếu bạn vay mua ô tô với lãi suất đơn, nhìn chung chi phí sẽ thấp hơn theo thời gian so với vay với lãi suất kép. Ngược lại, khi nói đến các sản phẩm đầu tư hoặc tiết kiệm, bạn sẽ muốn lãi suất kép vì tiền của bạn sẽ tăng trưởng nhanh hơn.

Biết rõ về lãi suất và cách nó tác động đến các quyết định tài chính của bạn sẽ giúp bạn tạo ra các chiến lược tài chính tốt hơn, cho dù đó là lập kế hoạch nghỉ hưu, tiết kiệm để mua nhà, gia tăng tài sản hay vay tiền.

Lãi đơn hay lãi kép, cái nào tốt hơn?

Điều này phụ thuộc vào việc bạn đang đầu tư hay vay nợ. Lãi kép khiến tiền gốc tăng theo cấp số nhân vì lãi suất được tính dựa trên cả lãi suất tích lũy theo thời gian lẫn tiền gốc ban đầu. Nó sẽ giúp tiền của bạn tăng trưởng nhanh hơn trong trường hợp đầu tư tài sản. Tuy nhiên, lãi kép có thể tạo ra hiệu ứng lăn cầu tuyết đối với khoản vay, và làm tăng nợ của bạn theo cấp số nhân. Bạn sẽ trả ít hơn theo thời gian với lãi suất đơn nếu bạn vay nợ.

Một số sản phẩm tài chính nào sử dụng lãi suất đơn?

Một số khoản vay cá nhân và các sản phẩm tiêu dùng đơn giản hơn sử dụng lãi suất đơn. Hầu hết các tài khoản tiền gửi ngân hàng, thế chấp, thẻ tín dụng và một số hạn mức tín dụng có xu hướng sử dụng lãi suất kép.

Lãi suất kép được tính như thế nào?

Kỳ tính lãi kép có thể là hàng ngày, hàng tháng, hàng quý hoặc hàng năm. Số kỳ càng cao, hiệu quả tính lãi kép càng lớn.

Lãi kép có được coi là thu nhập không?

Có. Lãi kép của một số loại hình đầu tư, chẳng hạn như tài khoản tiết kiệm hoặc trái phiếu, được coi là thu nhập.

Kết luận

Hãy để phép màu của lãi kép phát huy tác dụng bằng cách đầu tư thường xuyên và tăng tần suất trả nợ. Việc làm quen với các khái niệm cơ bản về lãi đơn và lãi kép sẽ giúp bạn đưa ra quyết định tài chính tốt hơn, tiết kiệm hàng ngàn đô la và tăng giá trị tài sản ròng theo thời gian.

THEO INVESTOPEDIA